Overfitting
- A hypothesis $h \in H$ is said to overfit the
training data if there exists some alternative hypothesis $h'
\in H$, such that $h$ has smaller error than $h'$ over the
training examples, but $h'$ has smaller error than $h$ over
the entire distribution of instances.
- That is, if
\[ error_{train}(h) < error_{train}(h') \]
and
\[ error_{D}(h) > error_{D}(h') \]
- This can happen if there are errors in the training
data.
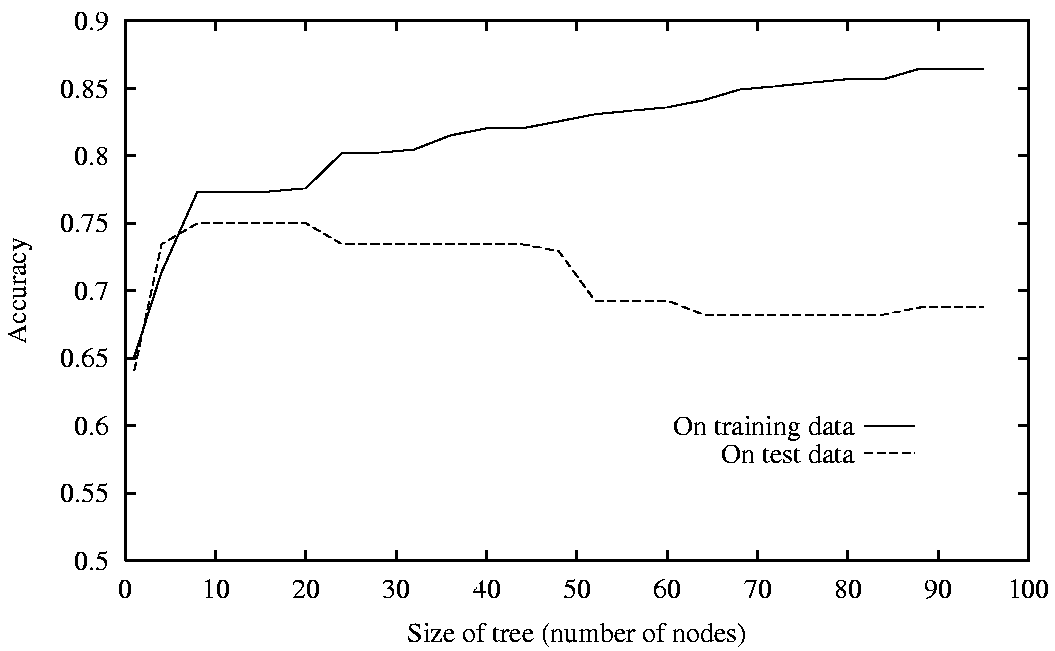
- It becomes worse if we let the tree grow to be too big, as
shown in this experiment:
José M. Vidal
.
18 of 25