Time Analysis

For the algorithm to work correctly, the time spent in metalevel thinking must be small compared to the time it takes to do an actual node expansion and propagation of a new solution (i.e. a PE(t,l)). Otherwise, the agent is probably better off choosing nodes to expand at random without spending time considering which one might be better.

A node expansion involves the creation of a new matrix M. If we assume that there are k agents and each one has n possible actions, then the number of elements in the matrix will be . Each one of these elements represents the utility of the situation that results after all the agents take their actions. In order to calculate this utility, it is necessary to simulate the new state that results from all the agents taking their respective actions (i.e. as dictated by the element's position in the matrix) and then calculate the utility, to some particular agent, of this new situation (see Figure 5). The calculation of this utility can be an arbitrarily complex function of the state, and must be performed for each of the elements in the matrix.

  
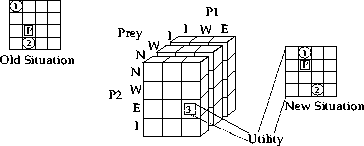
Figure 5: A very simplified version of the Pursuit Problem with only 3 agents and in a 4 by 4 grid. Given the old situation, each one of the elements of the matrix corresponds to the payoff in one of the many possible next situations. There is one for each combination of moves the agents might take (e.g. North, East, Idle). Sometimes, the moves of the predators might interfere with each other. The predator calculating the matrix has to resolve these conflicts when determining the new situation, before calculating its utility.

The next step is the propagation of the expected strategy. If we replace one of the ZK leaf strategies by some other strategy, then the time to propagate this change all the way to the root of the tree depends both on the distance between the root and leaf, and the time to propagate a strategy past a node. Because of the way strategies are calculated, it is almost certain that any strategy that is the result of evaluating a node will be a pure strategy. If all the children of a node are pure strategies, then the strategy the node evaluates to can be found by calculating the maximum of n numbers. In other words, the k-dimensional matrix collapses into a one-dimensional vector. If c of the children have mixed strategies, we would need to add numbers and find the maximum partial sum. In the worst case, c=k-1, so we need to add numbers.

We can conclude that propagation of a solution will require a good number of additions and max functions, and these must be performed for each leaf we wish to consider. However, these operations are very simple since, in most instances, the propagation past a node will consist of one max operation. This time is small, especially when compared to the time needed for the simulation and utility calculation of different possible situations. A more detailed analysis can only be performed on an application-specific basis, and it would have to take into account actual computational times.