Decision Tree Learning

This talk is based on

• Tom M. Mitchell. Machine Learning. [1] McGraw Hill. 1997. Chapter 3.
• and his slides [2].

• Decision Trees are among the most widely used methods for inductive inference.
• It is a method for approximating discrete-valued functions.
• Robust to noisy data and can learn disjunctive expressions.
• The hypothesis is represented using a decision tree.

• Has been used for everything from medical diagnosis to assessing the credit risk of loan applications.
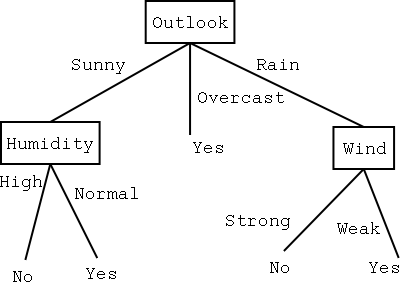
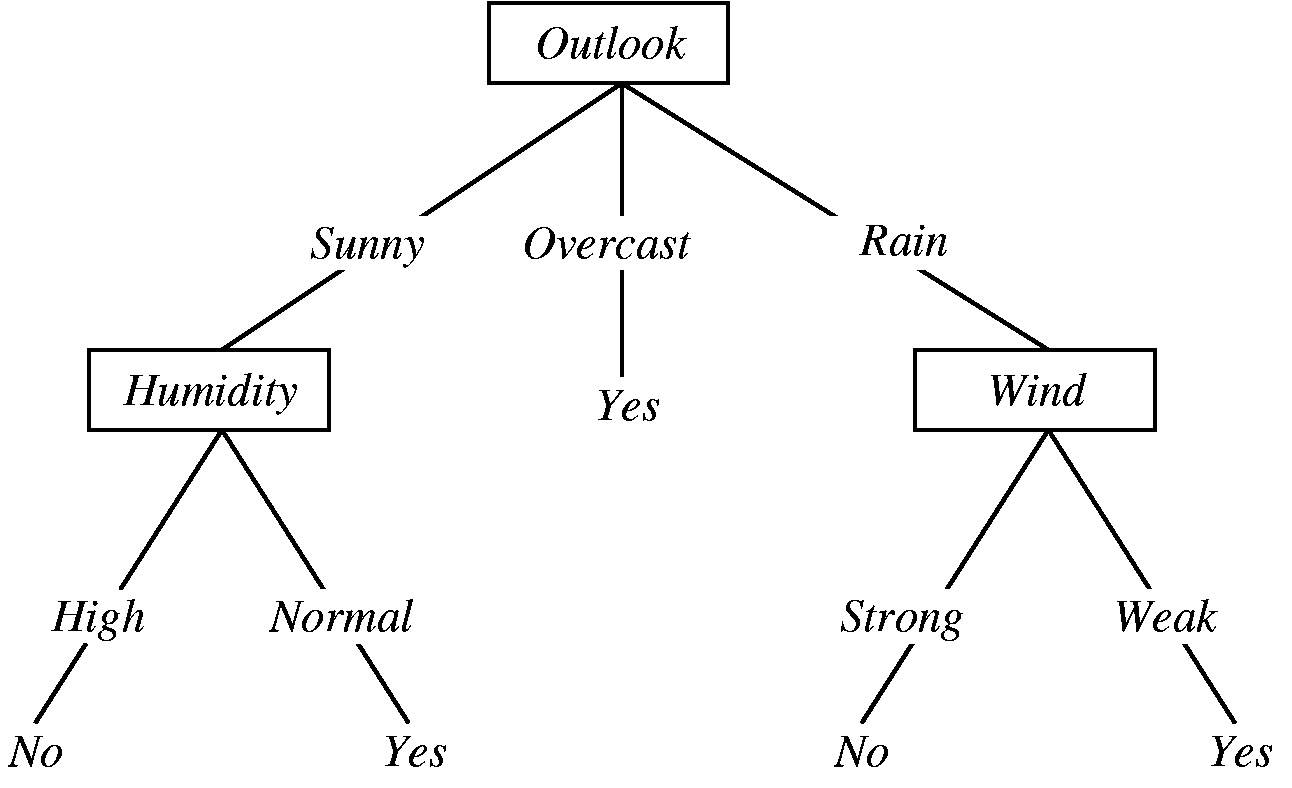
• Example: Tree to predict C-Section risk
• Learned from medical records of 1000 women.
• Negative examples are C-sections

[833+,167-] .83+ .17-
Fetal_Presentation = 1: [822+,116-] .88+ .12-
| Previous_Csection = 0: [767+,81-] .90+ .10-
| | Primiparous = 0: [399+,13-] .97+ .03-
| | Primiparous = 1: [368+,68-] .84+ .16-
| | | Fetal_Distress = 0: [334+,47-] .88+ .12-
| | | | Birth_Weight < 3349: [201+,10.6-] .95+ .05-
| | | | Birth_Weight >= 3349: [133+,36.4-] .78+ .22-
| | | Fetal_Distress = 1: [34+,21-] .62+ .38-
| Previous_Csection = 1: [55+,35-] .61+ .39-
Fetal_Presentation = 2: [3+,29-] .11+ .89-
Fetal_Presentation = 3: [8+,22-] .27+ .73-

• Each node in the tree specifies a test for some attribute of the instance.
• Each branch corresponds to an attribute value.
• Each leaf node assigns a classification.
• How would this tree classify: \[\langle Outlook=Sunny, Temperature = Hot, Humidity = High, Wind = Strong \rangle\]
• Decision trees represent a disjunction (or) of conjunctions (and) of constraints on the values. Each root-leaf path is a conjunction. \[ (Outlook=Sunny \wedge Humidity=Normal) \vee (Outlook = Overcast) \vee (Outlook=Rain \wedge Wind=Weak)\]

1. Instances describable by attribute-value pairs.
2. Target function is discrete valued.
3. Disjunctive hypothesis may be required.
4. Possibly noisy training data.
5. The training data may contain missing attribute values.

• Problems in which the task is to classify examples into one of a discrete set of possible categories are called classification problems.

• Basic Top-down algorithm:

1. $A \leftarrow$ the best decision attribute for next $node$.
2. Assign $A$ as decision attribute for $node$.
3. For each value of $A$, create new descendant of $node$.
4. Sort training examples to leaf nodes.
5. If training examples perfectly classified, Then STOP, Else iterate over new leaf nodes.

• This is basically the ID3 algorithm.
• What do we mean by best?

• There are 9 positive and 5 negative examples.
• Humidity = High has 3 positive and 4 negative.
• Humidity = Normal has 6 positive and 1 negative.
• Wind = Weak has 6 positive and 2 negative.
• Wind = Strong has 3 positive and 3 negative
• Which one is better as a root node, Humidity or Wind?

• $S$ is a sample of training examples
• $p_{\oplus}$ is the proportion of positive examples in $S$.
• $p_{\ominus}$ is the proportion of negative examples in $S$.
• Entropy measures the impurity of $S$ \[ Entropy(S) \equiv - p_{\oplus} \log_{2} p_{\oplus} - p_{\ominus} \log_{2} p_{\ominus} \]
• For example, if $S$ has 9 positive and 5 negative examples, its entropy is \[Entropy([9+,5-]) = -\left(\frac{9}{14}\right)\log_2\left(\frac{9}{14}\right) - \left(\frac{5}{14}\right)log_2\left(\frac{5}{14}\right) = 0.94\]
• This function is 0 for $p_{\oplus} = 0$ and $p_{\oplus} = 1$. It reaches its maximum of 1 when $p_{\oplus} = .5$
• That is, it is maximized when there degree of “confusion” is maximized.

• We can also say that $Entropy(S)$ equals the expected number of bits needed to encode class ($\oplus$ or $\ominus$) of randomly drawn member of $S$ using the optimal, shortest-length code.
• Why?
• Information theory: optimal length code assigns $- \log_{2}p$ bits to message having probability $p$.
• Imagine I'm choosing elements from $S$ at random and telling you whether they are $\oplus$ or $\ominus$. How many bits per element will I need? (We work-out encoding beforehand).
• If message has probability 1 then its encoding length is 0. Why?
• If probability .5 then we need 1 bit (the maximum).
• So, the expected number of bits to encode whether a random member of $S$ is $\oplus$ or $\ominus$ is: of $S$: \[ p_{\oplus} (-\log_{2} p_{\oplus}) + p_{\ominus} (-\log_{2} p_{\ominus}) \] \[ Entropy(S) \equiv - p_{\oplus} \log_{2} p_{\oplus} - p_{\ominus} \log_{2} p_{\ominus} \]

• If the target attribute can take on $c$ different values we can still define entropy \[Entropy(S) \equiv \sum_{i=1}^c -p_i\log_2p_i\]
• $p_i$ is the proportion belonging to class $i$.
• Now the entropy can be as large as $\log_2c$.

• The information gain is the expected reduction in entropy caused by partitioning the examples with respect to an attribute.
• Given $S$ is the set of example, $A$ the attribute, and $S_v$ the subset of $S$ for which attribute $A$ has value $v$: \[ Gain(S,A) \equiv Entropy(S) - \sum_{v \in Values(A)} \frac{|S_{v}|}{|S|} Entropy(S_{v}) \]
• That is, current entropy minus new entropy.
• Using our set of examples we can now calculate that
  • Original Entropy = 0.94
  • Humidity = High entropy = 0.985
  • Humidity = Normal entropy = 0.592
  • $Gain (S,Humidity) = .94 - \left(\frac{7}{14}\right).984 - \left(\frac{7}{14}\right).592 = .151$
  • Wind = Weak entropy = 0.811
  • Wind = Strong entropy = 1.0
  • $Gain (S,Wind) = .94 - \left(\frac{8}{14}\right).811 - \left(\frac{6}{14}\right)1.0 = .048$
• So Humidity provides a greater information gain.

ID3(Examples, Target, Attributes)
• Create a root node
• If all Examples have the same Target value, give the root this label
• Else if Attributes is empty label the root according to the most common value
• Else begin
  • Calculate the information gain for each attribute, according to the average entropy formula
  • Select the attribute, A, with the lowest average entropy (highest information gain) and make this the attribute tested at the root
  • For each possible value, v, of this attribute
    • Add a new branch below the root, corresponding to A = v
    • Let Examples(v) be those examples with A = v
    • If Examples(v) is empty, make the new branch a leaf node labeled with the most common value among Examples
    • Else let the new branch be the tree created by ID3(Examples(v), Target, Attributes - {A})
• end

• Again, using our examples, ID3 would first calculate
  • $Gain(S,Outlook) = 0.246$
  • $Gain(S,Humidity) = 0.151$
  • $Gain(S,Wind) = 0.048$
  • $Gain(S,Temperature)= 0.029$
• So, Outlook would be the root. The Overcast branch would lead to a Yes classification.
• At the Sunny branch we would recursively apply it for examples $S'= \{1,2,8,9,11\}$ leading to
  • $Gain(S', Humidity) = .97$
  • $Gain(S', Temperature) = .57$
  • $Gain(S', Wind) = .019$

• ID3 searches the space of possible decision trees: doing hill-climbing on information gain.
• It searches the complete space of all finite discrete-valued functions. All functions have at least one tree that represents them.
• It maintains only one hypothesis (unlike Candidate-Elimination). It cannot tell us how many other viable ones there are.
• It does not do back tracking. Can get stuck in local optima.
• Uses all training examples at each step. Results are less sensitive to errors.

• Given a set of examples there are many trees that would fit it. Which one does ID3 pick?
• This is the inductive bias.
• Approximate ID3 inductive bias: Prefer shorter trees.
• To actually do that ID3 would need to do a BFS on tree sizes.
• Better ID3 inductive bias: Prefer shorter trees over longer trees. Prefer trees that place high information gain attributes near the root.

• ID3 searches a complete hypothesis space but does so incompletely since once it finds a good hypothesis it stops (cannot find others).
• Candidate-Elimination searches an incomplete hypothesis space (it can only represent some hypothesis) but does so completely.
• A preference bias is an inductive bias where some hypothesis are preferred over others.
• A restriction bias is an inductive bias where the set of hypothesis considered is restricted to a smaller set.

• Occam's razor [3]: Prefer the simplest hypothesis that fits the data.
• Why should we prefer a shorter hypothesis?
• There are fewer short hypothesis than long hypothesis so
  • a short hypothesis that fits data unlikely to be coincidence
  • a long hypothesis that fits data might be coincidence.
• But, there are many ways to define small sets of hypothesis
  • e.g., all trees with a prime number of nodes that use attributes beginning with Z.
• What's so special about small sets based on size of hypothesis?

• How deep to grow?
• How to handle continuous attributes?
• How to choose an appropriate attributes selection measure?
• How to handle data with missing attributes values?
• How to handle attributes with different costs?
• How to improve computational efficiency?
• ID3 has been extended to handle most of these. The resulting system is C4.5 [4].

• A hypothesis $h \in H$ is said to overfit the training data if there exists some alternative hypothesis $h' \in H$, such that $h$ has smaller error than $h'$ over the training examples, but $h'$ has smaller error than $h$ over the entire distribution of instances.
• That is, if \[ error_{train}(h) < error_{train}(h') \] and \[ error_{D}(h) > error_{D}(h') \]
• This can happen if there are errors in the training data.
• It becomes worse if we let the tree grow to be too big, as shown in this experiment:

• Either stop growing the tree earlier or prune it after-wards. Pruning has been more effective.
• Use a separate set of examples (not training) to evaluate the utility of post-pruning nodes.
• Use a statistical test to estimate whether expanding a node is likely to improve performance beyond the training set.
• Use explicit measure of the complexity for encoding the training examples and the decision tree. Stop when this encoding size is minimize. Minimum Description Length principle (later).

• Split data into training and validation sets.

1. Do until further pruning is harmful:
   1. Evaluate impact on validation set of pruning each possible node (plus those below it)
   2. Greedily remove the one that most improves validation set accuracy

• Produces smallest version of most accurate subtree.
• Requires that a lot of data be available.

1. Infer tree as well as possible.
2. Convert tree to equivalent set of rules.
3. Prune each rule by removing any preconditions that result in improving its estimated accuracy.
4. Sort final rules by their estimated accuracy and consider them in this sequence when classifying.

• The tree on the left becomes the set of rules:

     IF $(Outlook=Sunny) \wedge (Humidity=High)$ 
     THEN $PlayTennis=No$
  
     IF  $(Outlook=Sunny) \wedge (Humidity=Normal)$
     THEN $PlayTennis=Yes$
  
     IF  $(Outlook=Overcast)$
     THEN $PlayTennis=No$
  
  ...and so on
  	  

• For example, we might have a Temperature attribute with a continuous value.
• Create a new boolean attribute that is true when the value is less than $c$ (the threshold).
• To pick $c$ sort the examples according to the attribute. Identify adjacent examples that differ in their target classification. Generate candidate thresholds at the midpoints.
• The candidate thresholds can be evaluated by computing the information gain associate with each one.
• The new discrete-valued attribute can then compete with the other attributes.

• The information gain tends to favor attributes with many values.
• One approach: use $GainRatio$ instead \[GainRatio(S,A) \equiv \frac{Gain(S,A)}{SplitInformation(S,A)} \] \[ SplitInformation(S,A) \equiv - \sum_{i=1}^{c} \frac{|S_{i}|}{|S|} \log_{2} \frac{|S_{i}|}{|S|} \] where $S_{i}$ is subset of $S$ for which $A$ has value $v_{i}$
• The $SplitInformation$ term discourages the selection of attributes with many uniformly distributed values.

• What if some examples are missing values of some $A$?
• Use training example anyway, sort through tree:
• If node $n$ tests $A$, assign most common value of $A$ among other examples sorted to node $n$, or
• assign most common value of $A$ among other examples with same target value, or
• assign fraction $p_{i}$ of example to each descendant in tree.
• Classify new examples in same fashion

• For example, in the medical field applying a test costs money, in a robotic setting applying a test takes time and power.
• How do we learn a tree that also minimizes cost?
• Replace gain by \[ \frac{Gain^{2}(S,A)}{Cost(A)}. \] or by \[ \frac{2^{Gain(S,A)} - 1}{(Cost(A) + 1)^{w}} \] where $w \in [0,1]$ determines importance of cost