| TargetShare: Resource Allocation in Dynamic Uncertain Domains | |||||
 |
New Ideas Targets/Resources negotiate for their own removal/consumption. Integration of Bayesian and market-oriented negotiation methods. Negotiation methods lead to dynamic self-organization by the agents. | ||||
Provide dynamic, distributed, and robust resource allocation. |
|
||||
| University of South Carolina: Mike Huhns (PI), Marco Valtorta, Juan Vargas, José M. Vidal | |||||
This research is part of the Ants project.
We propose the investigation and development of a novel hierarchical autonomous team approach to the tasking and allocation of military assets. Our research will make a fundamental change in the way targeting and logistics deployments are performed in military operations. This change is brought about by the use of negotiating agents to represent targets, as well as assets, in both tactical and strategic situations
We are designing and implementing a multiagent system (MAS) where each agent corresponds to either an agent in the problem domain (e.g., a weapon, such as a fighter) or a target. The MAS simulates all the important aspects of the problem domain. The agents form a focus for the computational work and embody the interests of the entity they represent. The agents also share the constraints and abilities of their entity.
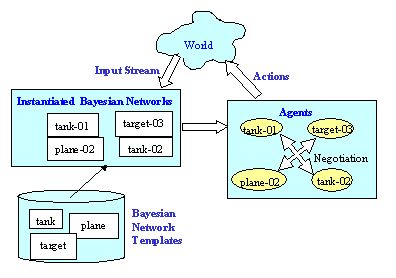
The basic architecture for our system presumes that there is a steady input stream of data coming from the "world." This stream collects all the information available. The information might come from a variety of sources, such as radar, satellite, military intelligence, etc. Importantly, some will be signal intelligence and some will be human intelligence. Since there are a number of sources, and not all of them are completely reliable, we can expect that there will be some noise, uncertainty, and even contradictions in the input data.
Not all agents will have access to all the available information. Information from sensors will be directed only towards the Bayesian networks that represent the agents that have access to that sensor information. For example, a plane might have information about the topology of a certain area, but a tank will have access to this information only if it can communicate with the plane.
Our Bayesian networks form the first line of defense against the noise in the input stream. The input data are used as values for the nodes in the instantiated Bayesian networks. We then propagate these values in order to determine which are the most probable states for each of the entities in the world. For example, two input sources might indicate that agent-01 has a high speed while a third input source indicates that it is stationary. The Bayesian networks would take this contradictory information, along with any other relevant data, and determine the most likely state of agent-01.
Bayesian networks offer an effective combination of clear semantics, efficiency, and formal representation of uncertainty. These representations are also well suited for integrating on-line information from diverse sources, including sonar, radar, images, tactical information, etc., and knowledge, expressed by domain experts or synthesized through discovery techniques. Bayesian networks are directed graphs that reflect mutual influences between collections of evidence and a set of hypotheses. Categorical random variables, represented as nodes in a graph, are interconnected by directed links that represent probabilistic dependencies. Each link signifies that the variable at the head of the arrow is conditionally dependent on the variable at the tail, while the lack of links between variables means direct conditional independence.
Several efficient algorithms have been developed for determining how an observation of subsets of variables (evidence) affect the probabilities of the remaining (query) variables. In essence, the arrival of new evidence updates probabilities at the observed variables and propagates through the graph until all variables are updated.
When new evidence arrives at any node, the probability assigned to the rest of the nodes in the network must be updated. This is normally done using message passing algorithms. At the end of the propagation, the network becomes a static snapshot that captures the most probable values of the variables in the domain at the time the observations were made. Bayesian networks can integrate disparate information, such as voice, video images, and tactical displays, with varying degrees of reliability.
As part of our efforts to better understand the complexity associated with time-dependent probabilistic inference, we are studying Bayesian filtering, which can be considered a generalization of Kalman filtering. The latter requires that the relationship between the measurement and the target state be linear, and that the measurement error be Gaussian, while the former relaxes both assumptions. The most general formulation of Bayesian filtering requires the definition of a likelihood function that represents the probability of sensor observation Y at time K, which in general depends on all the previous states. The complexity of this formulation has been recognized to be prohibitive. Therefore, a Markov condition is customarily assumed, which simplifies the problem and permits the evaluation of the posterior probability using efficient recursive methods. Bayesian filtering assumes that observations of continuous variables are made at finite, discrete intervals, but that the state space might be continuous. We can achieve further efficiency if we assume that both the observations and the state spaces are finite and discrete.
The model resulting from these assumptions is commonly known as the Hidden Markov Model (HMM), which we believe fits very well the challenge problem under study. Therefore, instead of requiring iterative numerical algorithms to evaluate the posterior probability of a target's trajectory, we could use dynamic programming algorithms, which require a quadratic number of operations.
Once the Bayesian network has produced a clear, though still probabilistic picture of the states of the entities, we give this information to the agents. The simulated agents embody their real-world entities and serve as a focus for the computations and negotiation. The agents then engage in a negotiation protocol in order to solve the problem of which agent(s) gets assigned to which target. Once the protocol stabilizes and the resource allocation problem is solved, the agents are ready to take action. These actions are taken in the real world and their results are fed back as input to the Bayesian network, starting again the same loop.
For example, In the sensor allocation problem each node is represented by an agent. These "sensor agents" are responsible for the creation of "target agents" which are, in turn, responsible for tracking the target using the Bayes network techniques described above. The target agents also engage in a bidding protocol with the sensor agents in order to obtain data from them. The application of this protocol results in sensors only scanning areas where the likelihood of finding or tracking a known target is high. This conserves resources while maximizing the accuracy of our predictions.
Specifically, we have run simulations which show that in the sensor allocation domain our bidding protocol will always find the optimal allocation, given enough time and communications bandwidth. We have also characterized how much time and communications bandwidth we will in different scenarios.
We are also pursuing further developments of Bayesian network and intelligent agent methodologies to support dynamic goal reassessment, anytime evaluation of reliability and value of information, agent-encapsulated Bayesian models, local and metalevel agent modeling, hierarchy of collaborating intelligent agents, and intelligent routing to reconfigure interagent information flow.