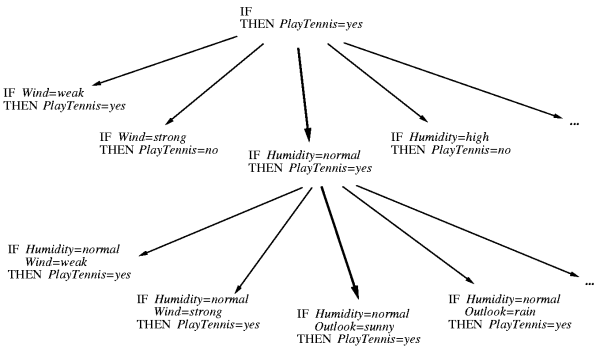
- Idea: organize the hypothesis space search in general to specific fashion.
- Start with most general rule precondition, then greedily add the attribute that most improves performance measured over the training examples.
IF Parent(x,y) THEN Ancestor(x,y)
IF Parent(x,z) ∧ Ancestor(z,y) THEN Ancestor(x,y)
;Examples is the set of examples;
; e.g.
; 1- Wind(d1)=Strong, Humdity(d1)=Low, Outlook(d1)=Sunny, PlayTennis(d1)=No
; 2- Wind(d2)=Weak, Humdity(d2)=Med, Outlook(d2)=Sunny, PlayTennis(d2)=Yes
; 3- Wind(d3)=Med, Humdity(d3)=Med, Outlook(d3)=Rain, PlayTennis(d3)=No
;Target_attribute is the one wish to learn.
; e.g. PlayTennis(x)
;Attributes is the set of all possible attributes.
; e.g. Wind(x), Humidity(x), Outlook(x)
; Threshold is the desired performance.
;
Sequential_covering (Target_attribute, Attributes, Examples, Threshold) :
Learned_rules = {}
Rule = Learn-One-Rule(Target_attribute, Attributes, Examples)
while Performance(Rule, Examples) > Threshold :
Learned_rules = Learned_rules + Rule
Examples = Examples - {examples correctly classified by Rule}
Rule = Learn-One-Rule(Target_attribute, Attributes, Examples)
Learned_rules = sort Learned_rules according to performance over Examples
return Learned_rules

Learn-One-Rule(target_attribute, attributes, examples, k)
;Returns a single rule that covers some of the Examples
best-hypothesis = the most general hypothesis
candidate-hypotheses = {best-hypothesis}
while candidate-hypothesis
;Generate the next more specific candidate-hypotheses
all-constraints = all "att.=val." contraints
new-candidate-hypotheses = all specializations of candidate-hypotheses by adding all-constraints
remove from new-candidate-hypotheses any that are duplicates, inconsistent, or not maximally specific
;Update best-hypothesis
best-hypothesis = $\argmax_{h \in \text{new-candidate-hypotheses}}$ Performance(h,examples,target_attribute)
;Update candidate-hypotheses
candidate-hypotheses = the k best from new-candidate-hypotheses according to Performance.
prediction = most frequent value of target_attribute from examples that match best-hypothesis
return IF best-hypothesis THEN prediction
Performance(h, examples, target_attribute)
h-examples = the set of examples that match h
return - Entropy(h-examples) wrt target_attribute
|
|
Performance(),
besides using entropy.This algorithm inductively learns a set of propositional if...then... rules from a set of training examples. To do this, it performs a general-to-specific beam search through rule-space for the "best" rule, removes training examples covered by that rule, then repeats until no more "good" rules can be found.
∀ x, y : Ancestor(x,y) ← Parent(x,y)
∀ x, y : Ancestor(x,y) ← Parent(x,z) ∧ Ancestor(z,y)
Ancestor(x,y) :- Parent(x,y)
Ancestor(x,y) :- Parent(x,z), Ancestor(z,y)
course(A) ← has-word(A, instructor) ∧ ¬has-word(A, good) ∧ link-from(A, B) ∧ has-word(B, problem) ∧ ¬link-from(B, C)
Female(Mary), ¬Female(x)
∀ x : Female(x) ∨ Male(x)
H ← L1 ∧ L2 ∧ ... ∧ Ln
A ← B ⇒ A ∨ ¬ Bso the horn clause above can be re-written as
H ∧ ¬L1 ∨ ¬L2 ∨ ... ∨ ¬Ln
L1θ = L2θ
Name(a) = Sharon, Mother(a) = Louise, Father(a) = Bob, Male(a) = False, Female(a) = True
Name(b) = Bob, Mother(b) = Nora, Father(b) = Victor, Male(b) = True, Female(b) = False, Daughter(a,b) = True
IF Father(a) = Bob ∧ Name(b) = Bob ∧ Female(a) THEN Daughter(a,b)
IF Father(x) = y ∧ Female(x) THEN Daughter(x,y)
Induction is, in fact, the inverse operation of deduction, and cannot be conceived to exist without the corresponding operation, so that the question of relative importance cannot arise. Who thinks of asking whether addition or subtraction is the more important process in arithmetic? But at the same time much difference in difficulty may exist between a direct and inverse operation; ... it must be allowed that inductive investigations are of a far higher degree of difficulty and complexity than any questions of deduction...
(Jevons 1874)
This talk available at http://jmvidal.cse.sc.edu/talks/learningrules/
Copyright © 2009 José M. Vidal
.
All rights reserved.
08 April 2003, 01:53PM