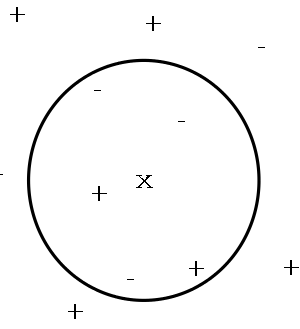
k-Nearest Neighbor Learning

Assume all instances correspond to point in n-dimensional space.
Store all training examples $\langle x_i, f(x_i) \rangle$.
Given that an instance $x$ is described by its feature vector \[ \langle a_1(x),a_2(x)\ldots a_n(x)\rangle \] we define the distance as \[ d(x_i,x_j) \equiv \sqrt{\sum_{r=1}^{n}(a_r(x_i)-a_r(x_j))^2} \]
Nearest Neighbor: To classify a new instance $x_q$ first locate nearest training example $x_n$, then estimate $\hat{f}(x_q) \leftarrow f(x_n)$
$k$-Nearest Neighbor Take a vote among the $k$ nearest neighbors, if discrete $f$. If continuous $f$ then take mean \[\hat{f}(x_{q}) \leftarrow \frac{\sum_{i=1}^{k}f(x_{i})}{k}\]