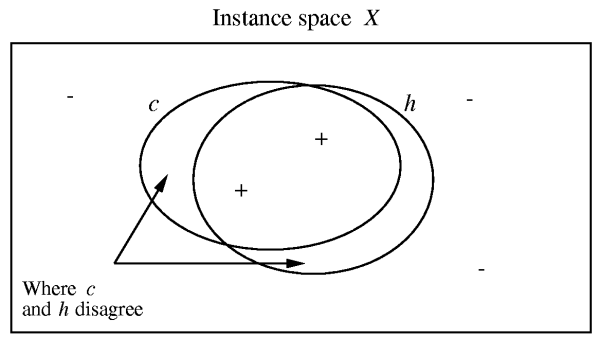
- The true error (denoted $error_{\cal{D}}(h)$) of hypothesis $h$ with respect to target concept $c$ and distribution $\cal{D}$ is the probability that $h$ will misclassify an instance drawn at random according to $\cal{D}$. \[error_{\cal{D}}(h) \equiv \Pr_{x \in \cal{D}}[c(x) \neq h(x)] \]
- That is, the proportion of hypotheses in the two identified areas to the left.
- The training error of $h$ with respect to $c$ represents how often it is wrong on the training data. That is, \[\Pr_{x \in \cal{D} \wedge x \in X}[c(x) \neq h(x)] \]
- We will start by assuming a training error of 0.