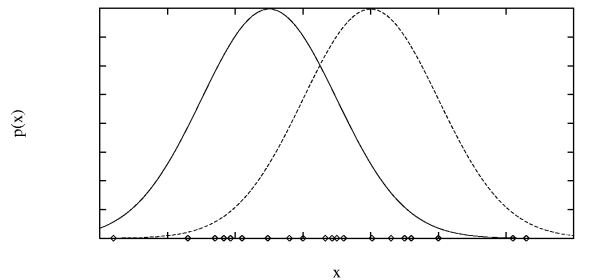
EM Example: Generating Data from k Gaussians
- Imagine the examples are generated by choosing instances
$x$ from $k$ Gaussians, with uniform probability.
- The learning task is to output a hypothesis that describes
the means $\langle \mu_1, \ldots, \mu_k \rangle$ of the $k$
distributions.
- We don't know which instance $x_i$ was generated by which Gaussian.
- We would like to find a maximum likelihood hypothesis for
those means, that is, the maximum likelihood estimates of
$\langle \mu_1, \ldots, \mu_k \rangle$.
- Think of full description of each instance as $y_i = \langle x_i, z_{i1}, z_{i2}
\rangle$, where
- $z_{ij}$ is 1 if $x_i$ generated by $j$th
Gaussian
- $x_i$ observable
- $z_{ij}$ unobservable
José M. Vidal
.
34 of 39