Each seller will try to predict what bid the other sellers will submit
(based solely on what they have bid in the past), and what bid the
buyer will likely pick. A complete implementation would require the
seller to remember past combinations of buyers, bids and results (i.e.
who was buying, who bid what, and who won). However, it is unrealistic
to expect a seller to remember all this since there are at least
possible combinations.
We believe, however, that the seller's one-level behavior can be
approximated by having him remember the last N prices accepted by
each buyer b for each good g, and form a probability density
function 
, which returns the probability that b will
accept(pick) price p for good g. Similarly, the seller remembers
other sellers' last N bids for good g and forms 
,
which gives the probability that s will bid y for good g. The
seller s can now determine which bid maximizes his expected profits.
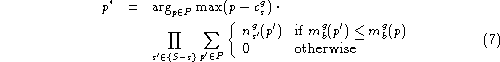
Note that this function also does a small amount of approximation by
assuming that s wins whenever there is a tie
. The function calculates the best
bid by determining, for each possible bid, the product of the profit
and the probability that the agent will get that profit. Since the
profit for lost bids is 0, we only need to consider the cases where
s wins. The probability that s will win can then be found by
calculating the product of the probabilities that his bid will beat
the bids of each of the other sellers.