EECE 352: Exam 2

I understand that it is the responsibility of every member of the Carolina community to uphold an maintain the academic standards and integrity of the University of South Carolina. Any member of the University community, who has reasonable grounds to believe that an infraction of the Code of Student Academic Responsibility has occurred, has an obligation to report the alleged violation.

I certify that I have neither given nor received unauthorized aid on this exam.

1. (5%) What is the worst-case running time of quicksort?

   O(N2)
   

2. (5%) Write a list consisting of the numbers 1 thru 10 such that sorting that list with Quicksort and a pick-pivot function that always picks the third element will produce the worst possible run time.

   10 11 1 2 3 4 5 6 7 8 9
   
   The third element must me either 1 or 10, the fourth element must be
   2 or 9, and so on...
   

3. (10%) Will the following program compile? Will it run? Is the copy constructor correctly implemented? Is the destructor correctly implemented? If anything is wrong, please explain and show how to fix it.

   #include<vector>
   using namespace std;
   
   template <class T>
   class Node {
     T element;
     Node * next;
   public:
     Node(){};
     Node(const T & x, Node<T> * n = 0) : element(x), next(n) {};
     Node(const Node<T> & n) : element(n.element), next(n.next) {};
     ~Node() {
       delete next;};
   };
   
   int main() {
     Node<int> a(1);
     Node<int> b(2, &a);
     Node<int> c(3, &b);
   }
   
   It gives an access violation. If a is deleted first then, when b
   gets deleted it will try to delete a, which has already been deleted
   so we get an access violation (or segmentation fault, or
   whatever...the program crashes.
   
   There are two ways to fix it. One way is just to get rid of the delete 
   in the destructor, the other way is to make the copy constructor
   actually copy the contents of n.next. Either way gets full credit. The 
   best way will depend on how this class will be used.
   
   Also, main should return a int. I did not take points for this.
   

4. (10%) Given the code below, implement the function eliminateNth(int n), which deletes the Nth element (starting from 0) from the list. Make sure you do not cause any memory leaks.

   using namespace std;
   
   template <class T>
   class Node {
   public:
     T element;
     Node * next;
     Node(){};
     Node(const T & x, Node<T> * n = 0) : element(x), next(n){};
   };
   
   template <class T>
   class List {
     Node<T> * root;
   public:
     List() : root(0){};
     List(Node<T> * r) : root(r) {};
     void eliminateNth(int n);  // implement this
   };
   
   template <class T>
   void List<T>::
   eliminateNth(int n){
     Node<T> * prev = root;
     if (n == 0) { //special case, not graded for
       Node<T> *old = root;
       root = root->next;
       delete old;
       return;
     }
     int i = 0;
     for (Node<T> *nd = root; nd !=0; ++i, prev = nd, nd = nd->next){
       if (i == n) {//delete this node
         prev->next = nd->next;
         Node<T> *temp = nd->next;
         delete nd;
         nd = temp;
         return;
       }
     }
   }
   
   Some of you did not check if n was bigger than the size of the list,
   or if n==0 (special case). I did not take points off for that.
   
   

5. (10%) Assume that you are given an already implemented stack class, with a header file as shown below (similar to the one in the book). All the functions you see are already defined so you can use them. Now, you will write a new class called "FinickyStack" which inherits from Stack. FinickyStack only pushes an element into the stack if it is bigger than than the element at the top. Implement the FinickyStack class.

   template <class Etype>
   class Stack
   {
   public:
     Stack( );
     ~Stack( ) { delete [ ] Array; }
     
     virtual void Push( const Etype & X );
     virtual void Pop( );
     virtual const Etype & Top( ) const;
     virtual int IsEmpty( ) const { return TopOfStack == -1; }
     virtual int IsFull( ) const  { return 0; }
     void MakeEmpty( )    { TopOfStack = -1; }
   private:
     int MaxSize;
     int TopOfStack;
     Etype *Array;
   };
   
   template <class Etype>
   class FinickyStack
   {
     virtual void Push( const Etype & X ) {
       if (x <= Top())
         return;
       Stack::Push(X);
     }
   }
   
   Notice that TopOfStack is a private data member so you cannot access
   it directly.
   

6. (5%) What is the minimal set of operators that must be defined on an iterator? What does each one of them do?

    We need operator*, operator++, and operator!= (or operator==).
   
   operator* returns what the iterator is pointing at
   operator++ increments the iterator
   and operator!= compares it with some other iterator. (i.e. are we done).
   
   Many of you named the iterators used in the book. While I did not take
   points off for that I would like to remind you that those iterators
   are only used in that book. The C++ STL names the above iterators as
   the standard iterators. That is, these are the ones you have been
   using in all your PSs; these are the ones everyones uses; these are
   the ones that should be second nature to you.
   
   

7. (10%) Given the definition of a tree node below, write the series of statements you will need in order to build the tree pictured below. At the end, a Node named root should correspond to the root of the pictured tree.

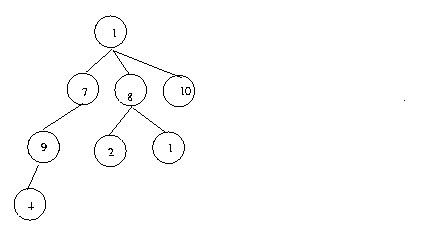
   template <class T>
   class Node {
   public:
     Node * firstChild;
     Node * nextSibling;
     T element;
     Node(const T & e, Node * f, Node * n) : element(e),
                          firstChild(f), nextSibling(n) {};
   }
   int main() {
       //write statements here
   
   
   int main(){
     Node<int> n4(4,0,0);
     Node<int> n9(9,&n4,0);
     Node<int> n1(1,0,0);
     Node<int> n2(2,0,&n7);
     Node<int> n10(10,0,0);
     Node<int> n8(8,&n2,&n1);
     Node<int> n7(7,&n9,0);
     Node<int> root(1,&n7, 0);
   }
   
   

8. (5%) Write out the nodes of the tree in the previous problem in post-order.

   Post-order means "first handle the children then the node" which leads 
   to:
   
   4 9 7 2 1 8 10 10
   
   I also accepted the incorrect "first handle the data members then the
   node" which leads to:
   
   4 9 1 2 10 8 7 1
   
   

9. (10%) Insert the list of numbers {5, 8, 4, 10, 13, 17, 2, 6, 7, 9} into a Binary Search Tree. Then delete the numbers {5, 4, 10}. Show the final tree after all the insertions are done, as well as the tree after each deletion.

   The solutions to this problem and the ones below will be posted
   outside my door by Monday.
   
   
   

10. (10%) Insert the list of numbers {15, 18, 25, 20, 21, 19, 27} into an AVL tree. Show the tree after each insertion. Specify what kind of rotations where performed after each insertion.

11. (10%) Insert the list of numbers {20, 15, 25, 10, 5, 12, 17, 18} into a top-down RedBlack tree. Show the tree after each insertion and specify which rotations and color changes where performed. You can draw red nodes as squares and black nodes as circles.

12. (10%) Insert the list of numbers {20, 7, 30, 10, 9, 25, 22} into an AA tree. Show the tree after each insertion and each skew or split, specifying which one you performed.